二叉搜索树(binary search tree)支持许多动态集合操作,包括插入节点构建树,查找(最大值,最小值,前驱,后继,指定值)节点,遍历(前中后序遍历)树,删除节点等。在树上进行的操作所花费的时间与树的高度成正比,对于有n的节点的一个完全二叉树,这些操作的最坏运行时间为Θ(lg n).但是如果这棵树是一个n个节点连接而成的线性链,那么同样的操作的最坏运行时间就为Θ(n).为了尽量避免这种低效的二叉树,可以在构造树时采用随机构造的方式。随机构造的二叉树的期望高度O(lg n),因此在这样的一棵二叉树上的操作的平均运行时间就为Θ(lg n).但实际上,随机化的构造树的方式也不能完全杜绝最坏情况的出现,所以还有一些二叉搜索树的变种,如红黑树,B树等,他们可以保证基本操作具有好的最坏情况性能。
在本文中,不讨论红黑树和B树,我们只讨论二叉搜索树的各种操作。
什么是二叉搜索树?
一棵二叉搜索树就是以一个二叉树来组织的,树上的每一个节点就是一个对象,对象中除了key和卫星数据之外,还有用于维护二叉树结构的三个属性left,right,parent(在c语言中他们是三个指针),他们分别指向节点的左孩子,右孩子和父节点。其中key被称为节点的关键字,它是二叉搜索树中确定节点之间大小关系的关键属性,一般可以设置为整型类型。如果某一个节点的没有左孩子,右孩子或父节点,那么就将对应的属性指针置空即可。该树的根节点是整棵树中唯一一个parent属性为空的节点。这些置空的指针通常被用来确定树的边界。二叉搜索树之所以可以具有灵活高效的操作,是因为它具有如下的性质:
- 如果节点的左子树不空,则左子树上所有结点的值均小于等于它的根结点的值;
- 如果节点的右子树不空,则右子树上所有结点的值均大于等于它的根结点的值;
- 任意节点的左、右子树也分别为二叉搜索树
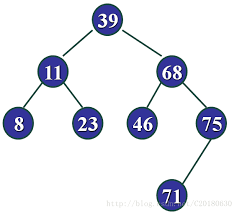
二叉搜索树的基本操作
本文重点讨论的就是二叉搜索树上的操作,下面我们来逐一的讨论。首先声明:为了减少讨论的复杂度,假设树上的所有节点的关键字均不相同,下面我的代码也基于此,对于节点关键字有重复的情况,调整代码即可。下面我们先定义节点的数据结构:
1 | typedef struct node{ |
构建
我们想要实现在二叉搜索树上的操作,那么首先我们就需要构建出一棵二叉搜索树.我们可以从一个数组中构建二叉搜索树,逐个的从数组中读取数据,然后以插入的方式将数据插入到树中,即我们需要一个将数据插入到树中的操作。
插入
递归插入
1 | /** |
非递归插入
1 | /** |
构建二叉查找树
1 | void init_bst(BST_p& root,int * a ,size_t size){ |
有了上面的这几个函数,我们就可以像下面这样来构建一个二叉搜索树:
1 |
|
遍历
二叉搜索树的性质允许我们通过一个简单的递归算法来按序输出二叉搜索树中的所有关键字,这种算法称之为中序遍历(inorder walk tree),这样命名的原因是输出的子树根的关键字位于其左子树的递归调用语句和右子树的递归调用语句之间。类似的先序遍历,后续遍历也是根据关键字输出语句与其左右子树递归调用语句之间的先后关系确定的。
下面是三种遍历的代码:
1 | /** |
上述代码中的中序遍历可以按照从小到大的顺序依次输出树中所有节点的关键字。
查找
在二叉查找树中可以快速的查找元素,下面我们就来看看在二叉查找树中各种查找操作都是如何进行的。
查找最大值与最小值
找具有最值关键字的节点在二叉查找树中非常的直接。比如要找具有最小关键字的节点,我们可以从根节点一直向左查找,如果一个节点具有左孩子,那么它的左孩子的关键字一定比它本身的关键字小,这时就可以迭代的去查看其左孩子,直到某一节点的左孩子为空,这样就是找到了树中最左边的节点,也就具有最小关键字的节点。上述寻找最小值的代码如下:
1 | /** |
同理,找最大值的代码如下:
1 | /** |
查找前驱与后继
给定一棵二叉搜索树中的节点,有时需要按照中序遍历的次序(从小到大)查找它的后继(successor)或前驱(predecessor)。找前驱和后继在逻辑上是对称的,我们这里以找一个节点的后继节点作为例子讲解。按照定义我们可以知道,找节点a的后继节点就是找树中关键字比a的关键字大的所有节点中的最小关键字节点(虽然很绕,但就是这个道理:)。如何才能找到它呢?我们需要分两种情况讨论:
给定的节点a具有右孩子
在这种情况下,a的后继节点必定存在于a的右子树中,并且为右子树中的关键字最小节点。给定的节点a没有右孩子
在这种情况下,a的后继节点在哪里呢?为了找到a的后继节点,我们就要从a节点开始追根溯源,向上找它的祖先,直到找到第一个这样的祖先s:s的左孩子s’也是a的祖先,那么节点s就是这种情况下a的后继节点。
下面是上述两种找后继节点的示意图。声明:这两张图片借自别人的博客(读书人的东西怎么能叫偷呢:)!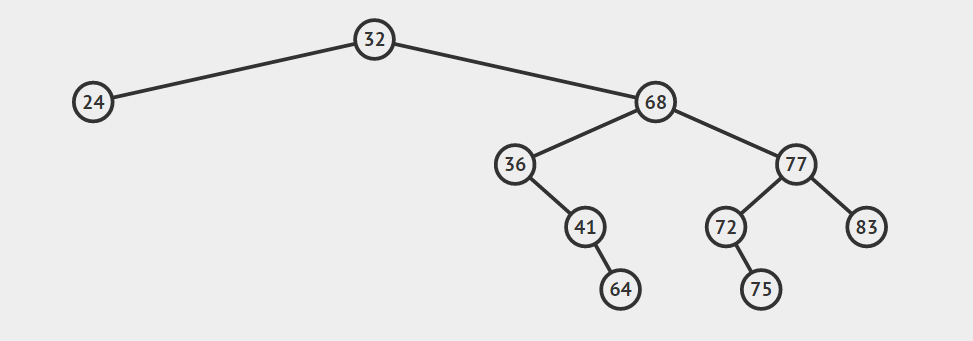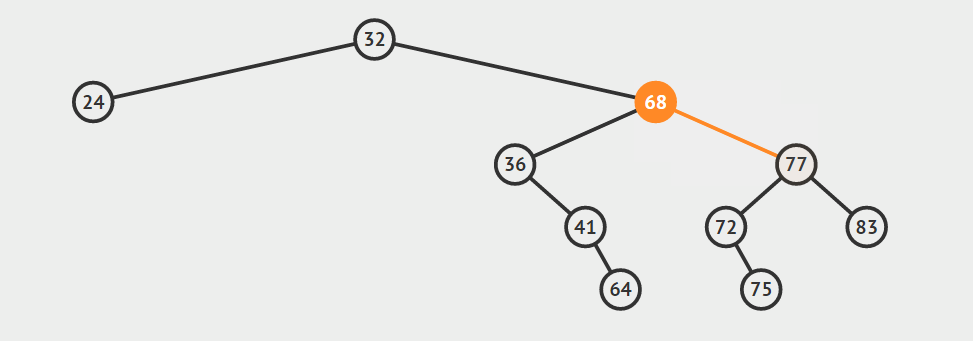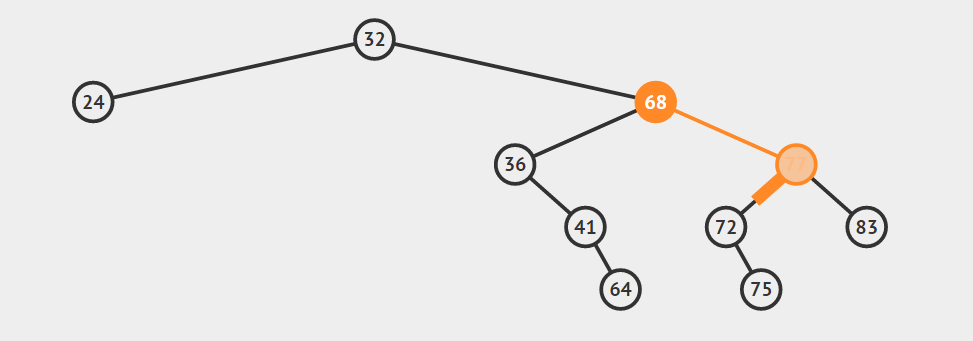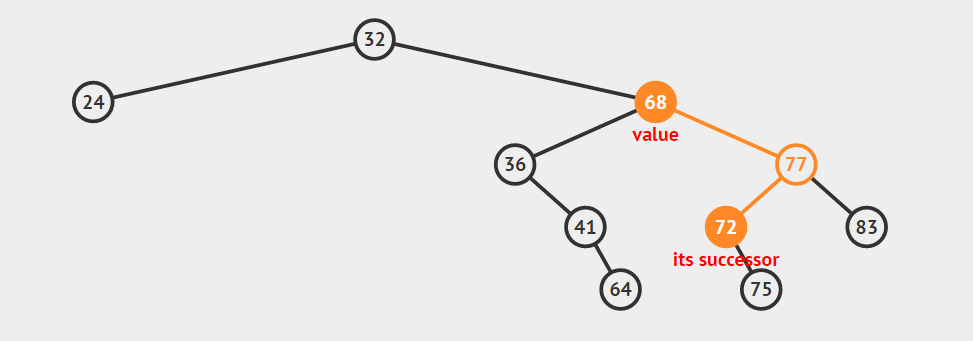
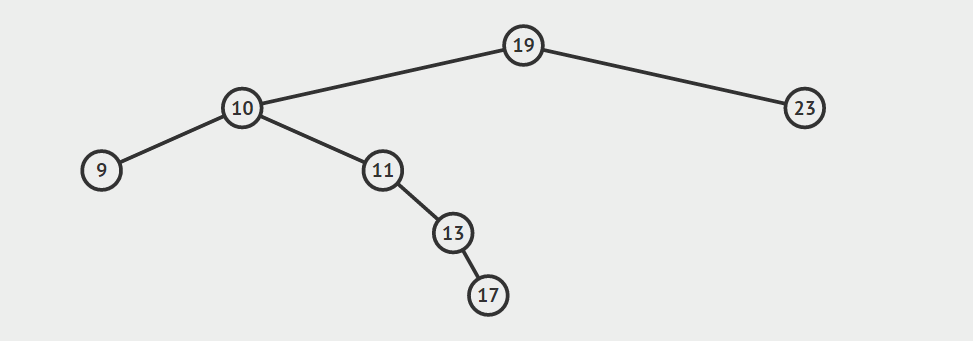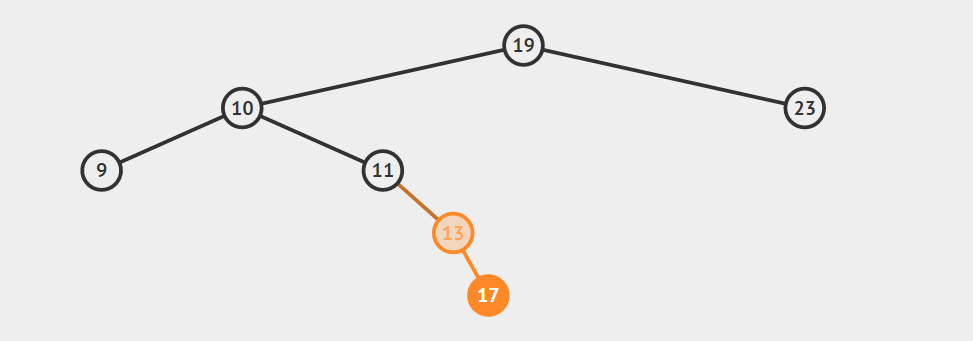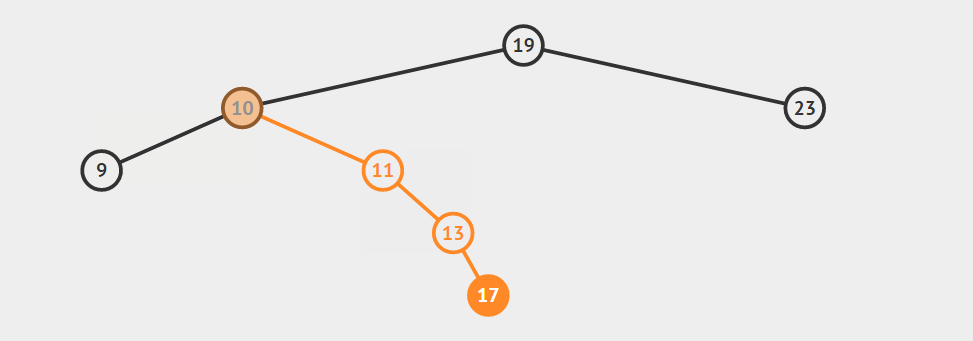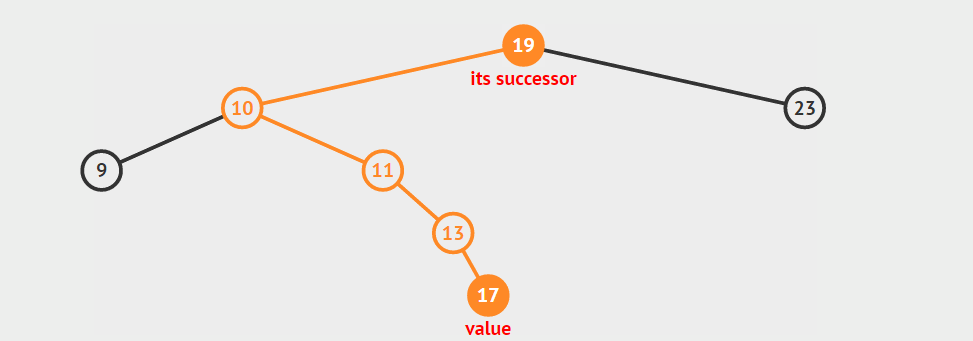
下面是找后继节点的代码:
1 | BST_p successor(BST_p node){ |
找前驱节点的代码:
1 | BST_p perdecessor(BST_p node){ |
查找具有指定关键字的节点
给定一个节点和一个关键字的值,找到树中关键字的值与给定值相等的节点。这个可以用递归和非递归两种方式实现。
递归
1 | /** |
非递归
1 | /** |
删除
给定一个树中的节点a,要求删除该节点并且保持二叉搜索树的结构。删除这一操作根据给定节点a的情况的不同,可分成一下三种情况讨论:
- 节点a没有孩子节点
对于节点a没有孩子节点的情况,我们只需要做以下操作:通过比较a节点的关键字与其父结点的关键字大小从而确定a节点是其父结点的左孩子还是右孩子,然后将a的父节点的对应指针置空,并且释放a所指向节点所占用的内存。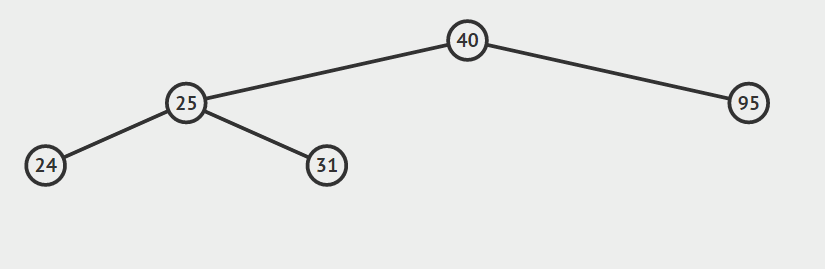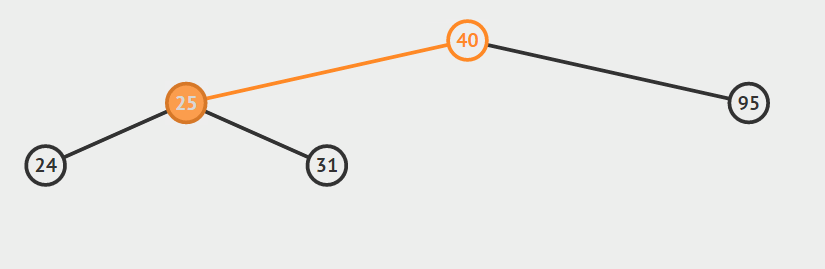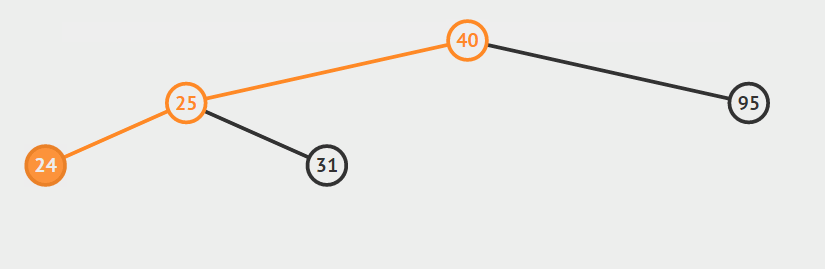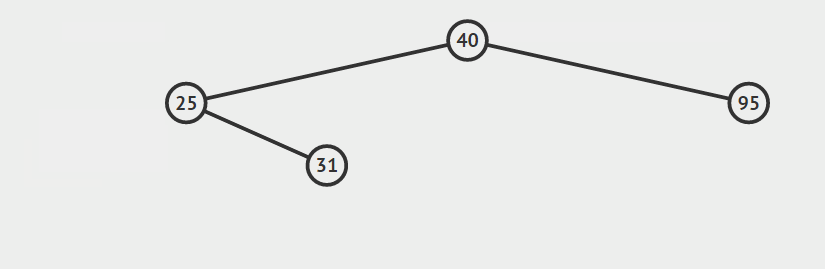
- 节点a只有一个孩子节点
对这种情况,首先要确定a是其父结点的左孩子还是右孩子,然后根据此信息将a的父节点的对应指针指向a的那个唯一的孩子节点,并且将a的孩子节点的父指针指向a的父节点,最后释放a所指向的节点占用的内存。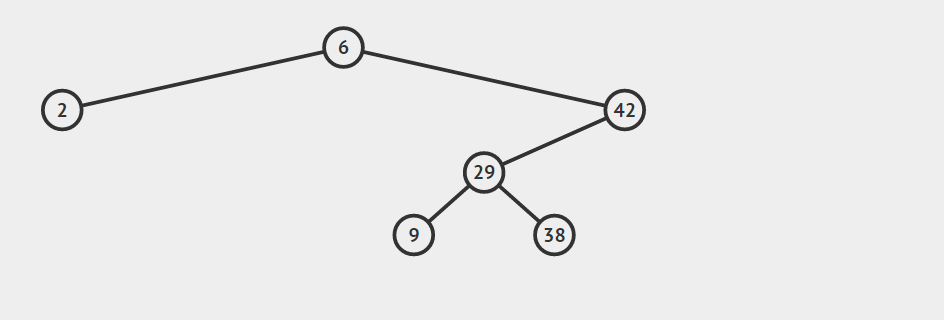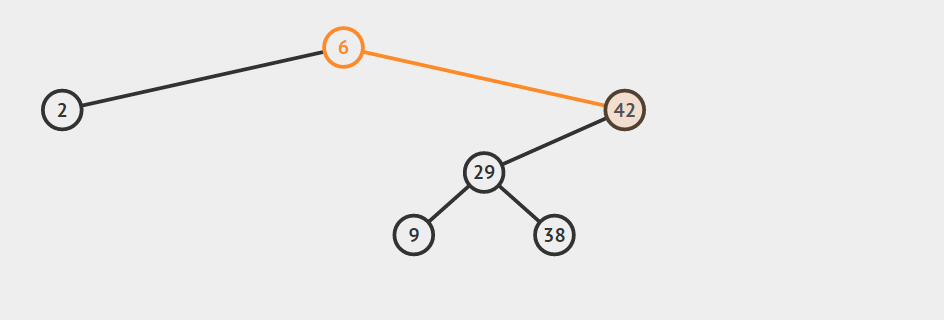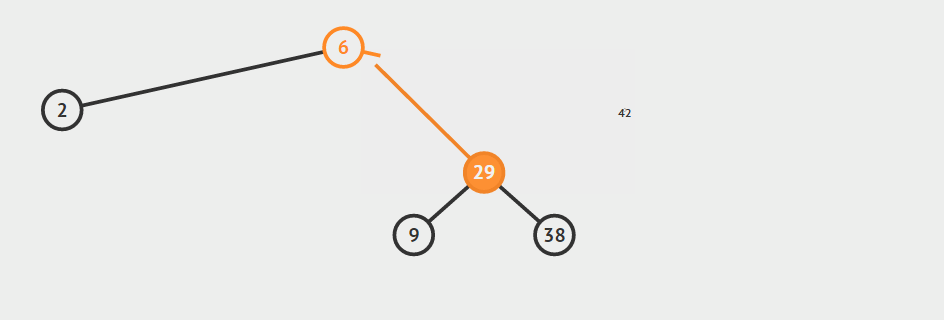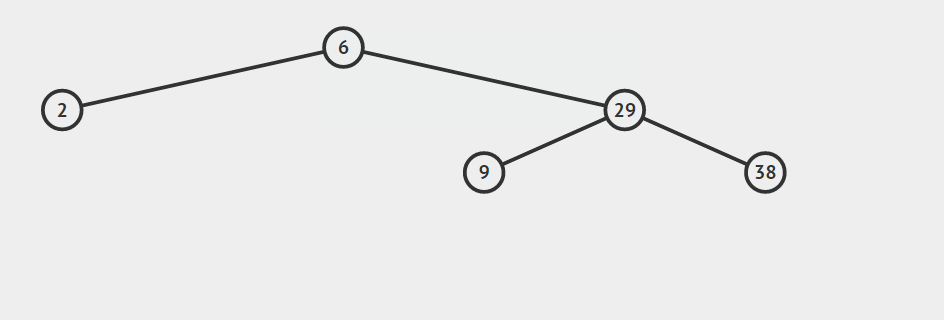
- 节点a有两个孩子节点
首先找到节点a的后继节点b,然后根据b是否是a的右孩子分两种情况讨论:
1.b是a的右孩子
如果b是a的右孩子,将b提升到a节点的位置,并且将原来a节点的左子树,连接到b节点的左支上(b节点的左支初始时为空),最后释放a所指向的节点的内存。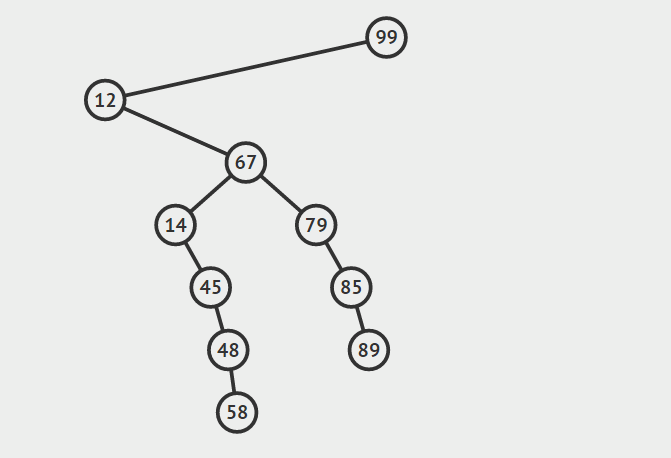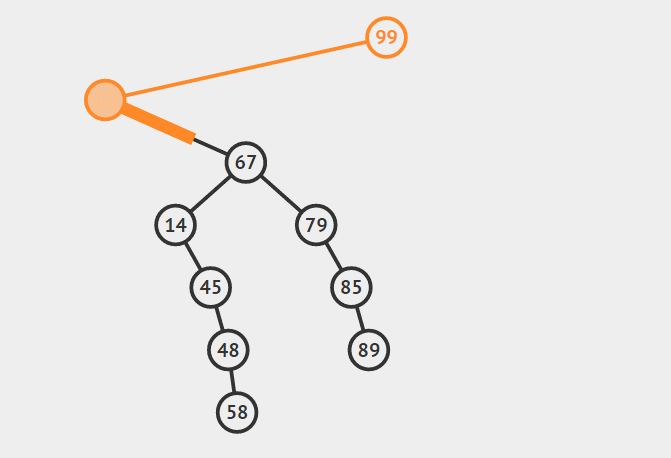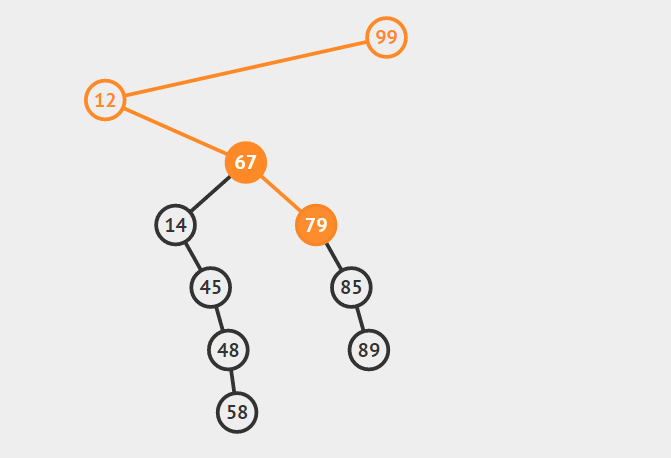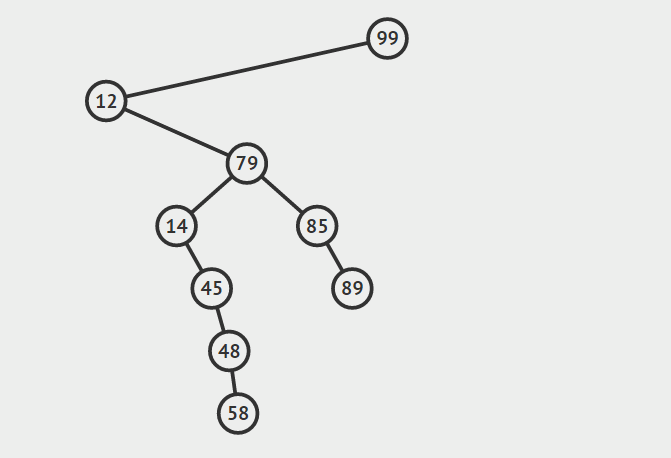
2.b不是a的右孩子
首先将b节点的右孩子提升到b的位置,即将b的右孩子连接到b的父节点的左支上(想一想为什么一定是左支上呢?因为b是a的后继节点,而且现在的讨论又是在b不是a的右孩子的基础上)。然后将原来a节点的左子树连接到b节点的左支上(该支初始时为空),最后将b提升到a的位置,并且释放a节点占用的内存。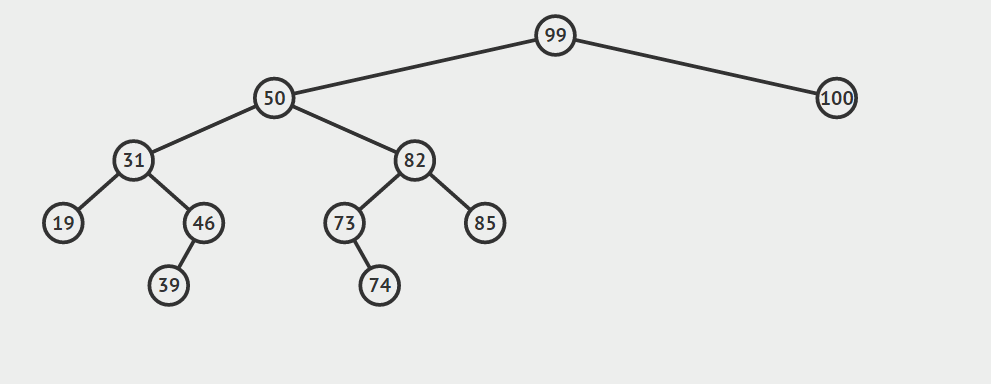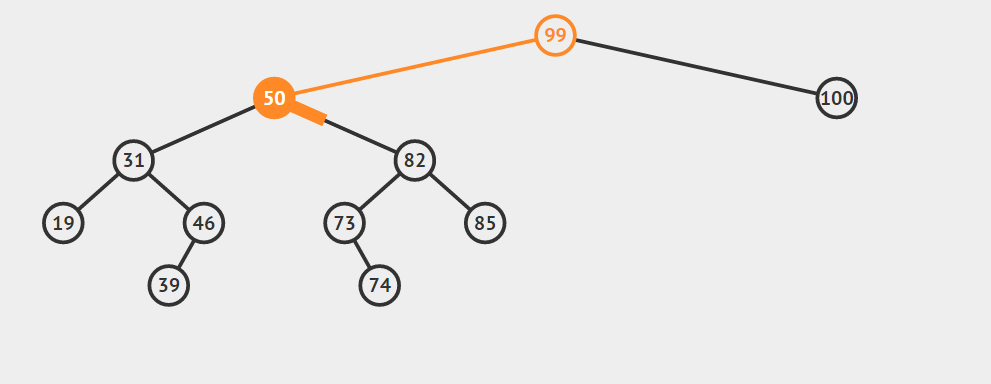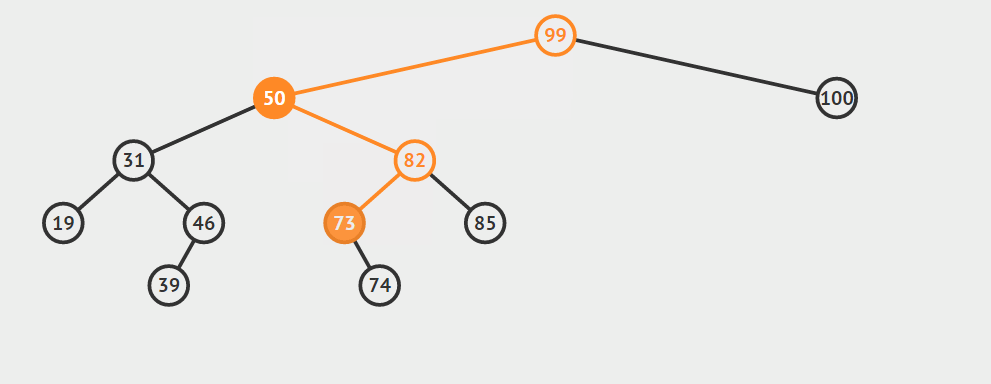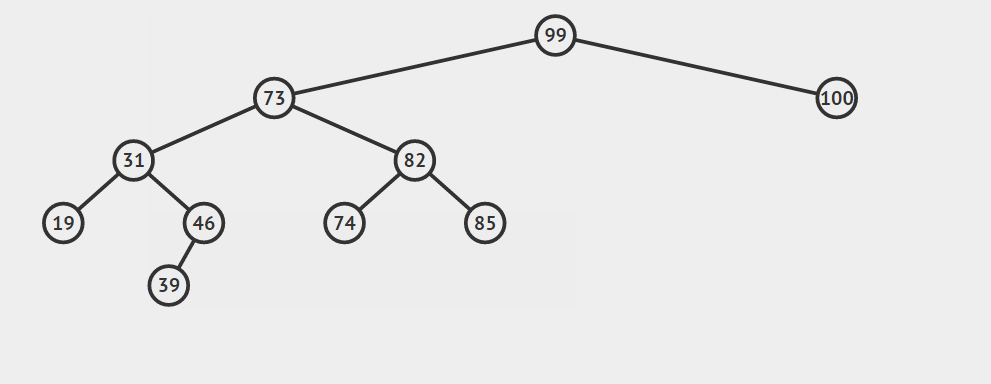
1 | /** |
随机构建
在文章开头介绍了,如果一棵二叉树是一个n个节点连接而成的线性链,那么该二叉树的效率就极其的低下,它就与链表无异了,无法发挥出搜索二叉树的威力。就拿我们上面的init_bst函数为例吧,我们是以用户提供的数组来初始化我们的二叉搜索树的,假如用户提供了这样的一个数组{1,2,3,4,5},或者是这样的{9,8,6,4,3,2},大家想想我们给构造出来的是一什么样的二叉树呢?第一个数组构造出来的二叉搜索树的每个节点只有右孩子没有左孩子,而第二个构造出来的二叉搜索树的每个节点则只有左孩子没有右孩子。这就是极其低效的二叉树。怎样去避免这样的问题呢?
显然,我们不应该对用户的输入做任何限制,那么我们就只能改变自己来适应用户了:)。我们可以在用户提供的数组中通过不重复无遗漏的随机取元素的方法来构造一个随机序列,然后用该序列来构造一个随机二叉搜索树。代码如下:
1 | void swap(int &a, int &b) { |
上述随机构建二叉搜索树的方法,在初始化构建树的时候,确实可以降低因用户给定的数组有序而创建低效二叉搜索树的情况,但是它无法做出保证。并且我们在对二叉搜索树这一动态集合进行插入删除等动态操作时,搜索二叉树的形态仍然可能走向低效。前面的动态操作会降低后面操作的效率。怎么办呢?这就要看其他的一些二叉搜索树的变体了!
参考
Introduction to Algorithm (Third Edition)
多动态图详细讲解二叉搜索树聪聪的个人网站
二叉查找树(BST) | 神奕的博客