平衡二叉树(AVL)

上文中谈到朴素的二叉搜索树在进行插入节点，删除节点等动态操作的时候会影响到树的形态，可能致使树走向低效，影响后续操作的效率。今天就介绍一下二叉搜索树的一个变种——平衡二叉树(AVL)。AVL树是一种自平衡的二叉搜索树，在进行动态操作时可以维持自身形态的平衡，从而保证基本操作的时间复杂度维持在O(logn)。
下图为一个低效的二叉查找树的示意图，它已经退化成了链表，完全失去了二叉查找树的优势。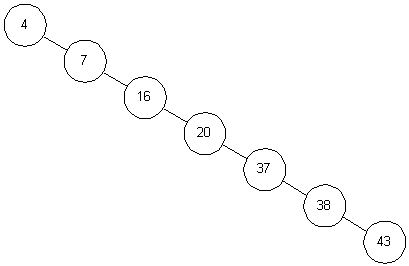

什么是平衡二叉树？

1962年，Adelson-Velsikii和Landis提出了一种结点在高度上相对平衡的二叉查找树，又称为AVL树。其平均和最坏情况下的查找时间都是O(logn)。同时，插入和删除的时间复杂性也会保持O(logn)。平衡二叉树的定义如下:

• 它或者是一棵空二叉树。
• 或者是具有如下性质的二叉查找树：其左子树和右子树都是高度平衡的二叉树，且左子树和右子树的高度之差的绝对值不超过1。

如果将二叉树上结点的平衡因子BF（Balanced Factor）定义为该结点的左子树与右子树的高度之差，根据AVL树的定义，AVL树中的任意结点的平衡因子只可能是-1（右子树高于左子树）、0或者1（左子树高于右子树）。

AVL树通过为每个节点设置并维护一个height(当前节点的高度)属性并且在执行动态操作的时候监控平衡因子BF的值，来监控自身的形态变化，从而实现自平衡。在动态操作执行后，如果某一个节点的BF值不在正常范围内(-1,0,1)时,AVL树自身可以通过旋转来调整子树的高度，使不符合AVL定义的部分重新符合定义。

平衡二叉树的基本操作

平衡二叉树本质上还是一棵二叉搜索树，所以在大多数的操作上两者是几乎相同的。唯一不同的是平衡二叉树在插入节点和删除节点等动态操作上增加了自平衡的操作(通过旋转)。以免和上一篇文章重复，在这里我们只讨论平衡二叉树的插入和删除操作。

要想实现平衡二叉树的带自平衡功能的插入和删除操作，我们首先要来研究一下AVL实现自平衡的机制－－旋转。

首先定义平衡二叉树节点结构体和几个功能宏函数：

#define HEIGHT(n) (((n) == NULL) ? 0 : (n)->h)
#define MAX(a, b) ((a) < (b) ? (b) : (a))

typedef struct avl_node{
    int key;
    int h;　//这里增加了h的属性，用来记录当前节点的高度
    struct avl_node *right;
    struct avl_node *left;
} node, *avl_node_ptr;

int get_bf(avl_node_ptr node){
    if(node==NULL)
        return 0;
    return HEIGHT(node->left)-HEIGHT(node->right);
}

旋转

在AVL树的平衡化操作中，存在两种基本旋转操作，左旋和右旋。在一次平衡化操作中，左旋和右旋这两个基本旋转操作可能被执行一次或多次。并且是从最小不平衡二叉树的根节点开始的。(即从离插入节点最近的，平衡因子超过1的祖先节点开始)

单旋转

1.右旋操作(LL_right_rotate)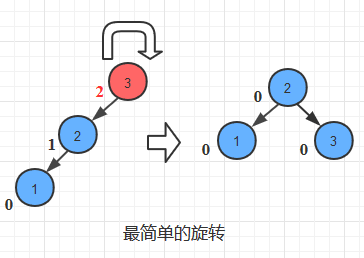

如上图，新插入了节点1,我们从新插入的节点开始向上寻找它的祖先节点，发现了第一个失衡节点3。也就找到了这里的最小不平衡二叉树就是以3为根节点的那棵树。也就是新插入的节点出现在失衡节点的左孩子的左子树上,此时我们需要对他们进行右旋操作(LL_right_rotate)。如上图，将根节点的左孩子2提升为新的根节点,而旧的根节点3则作为新根节点2的右孩子存在。

下面看一个复杂一些的需要右旋的情况：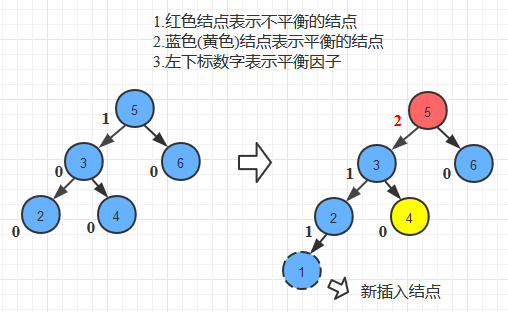

新插入的节点为1,同样的，我们从1开始依次向上检查其祖先节点，第一个找到了5是不平衡的节点。由于新插入的节点1出现在失衡节点5的左孩子的左子树上，我们需要对其进行右旋操作(LL_right_rotate)。但这种情况似乎与上面那种简单情形不同。具体的旋转细节如下: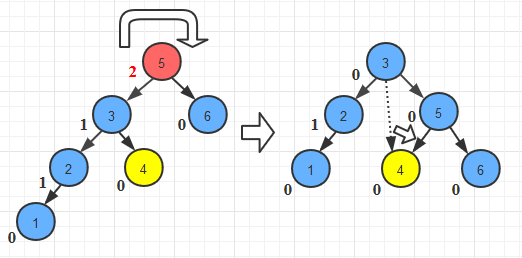

我们仍然是将失衡节点5的左孩子3提升为新的根节点，旧的根节点5则作为3的右孩子，所增加的是:还需要将新根节点3原本的右孩子作为旧根节点5的左孩子。

仔细分析发现，复杂情况中所增加的操作在简单情况中就是将NULL挂到NULL上，也就是说上面的简单的情形和复杂的情形的本质是统一的，我们可以将这两种情况总结成下面的代码：

//root为最小不平衡二叉树的根节点，插入的节点插在root的左孩子的左子树上
//需要将root的左孩子作为新的根节点,右旋
static avl_node_ptr LL_right_rotate(avl_node_ptr root){
    avl_node_ptr new_root = root->left;
    root->left = new_root->right;
    new_root->right = root;
    new_root->h = MAX(HEIGHT(new_root->left), HEIGHT(new_root->right)) + 1;
    root->h = MAX(HEIGHT(root->left), HEIGHT(root->right)) + 1;
    return new_root;
}

2.左旋操作(RR_left_rotate)
左旋和右旋是镜像对称的,当插入的节点位于离他最近的失衡节点的右孩子的右子树上时，我们就需要对其进行左旋操作(RR_left_rotate),示意图如下: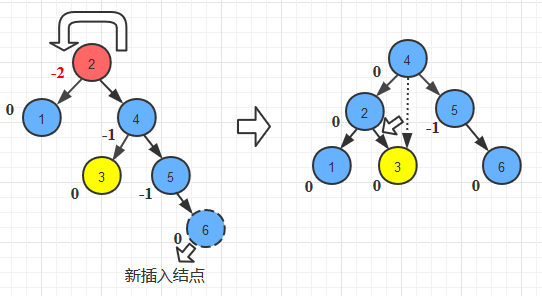

实现如下:

//插入的节点位于root的右孩子的右子树上，root的右孩子作为新的根节点，左旋
static avl_node_ptr RR_left_rotate(avl_node_ptr root){
    avl_node_ptr new_root = root->right;
    root->right = new_root->left;
    new_root->left = root;
    new_root->h = MAX(HEIGHT(new_root->left), HEIGHT(new_root->right)) + 1;
    root->h = MAX(HEIGHT(root->left), HEIGHT(root->right)) + 1;
    return new_root;
}

复合旋转

1.先左旋再右旋(LR_left_right_rotate)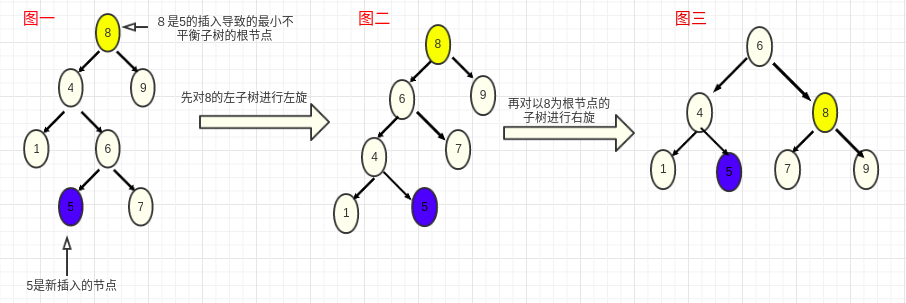

如上图所示，我们在树上插入了节点5,然后从5开始依次向上寻找失衡节点，找到失衡节点8,观察新插入的节点与该失衡节点的位置关系我们可以发现，新插入的节点位于其最近的失衡节点的左孩子的右子树上。这不是我们刚才讨论的单旋转中的任何一种情况，我们怎样才能将这种情况的树调整会平衡状态呢?如图，要调整这种情形，我们要首先将失衡节点的左子树进行左旋，然后对以失衡节点为根节点的树进行右旋
代码如下:

//新插入的节点位于root的左孩子rootl的右子树上，
//那么首先需要先对以rootl为根节点的子树进行左旋(RR_left_rotate)
//然后对以root为根节点的子树进行右旋(LL_right_rotate)
static avl_node_ptr LR_left_right_rotate(avl_node_ptr root){
    root->left = RR_left_rotate(root->left);
    return LL_right_rotate(root);
}

2.先右旋再左旋(RL_right_left_rotate)
下面的这种情况是插入节点出现在离他最近的失衡节点的右孩子的左子树上,和上面的情况是对称的，这里直接给出代码:

//同上
static avl_node_ptr RL_right_left_rotate(avl_node_ptr root){
    root->right = LL_right_rotate(root->right);
    return RR_left_rotate(root);
}

再平衡

上面在讨论旋转时讨论了四种失衡的场景以及每种场景对应的平衡调整方法，下面我们做个小小的总结:在代码中我们应该如何判定对应的失衡场景，又该如何调整呢？根据当前破坏平衡的结点的平衡因子，以及其孩子结点的平衡因子来判定，通过旋转来调整。

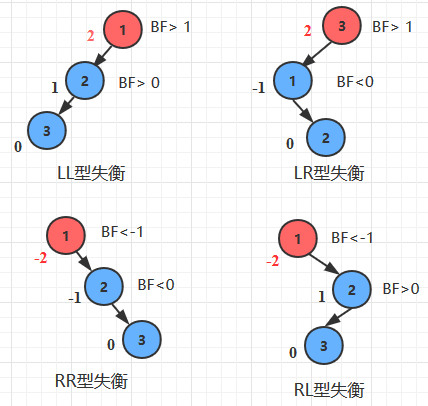
失衡场景	判定准则	调整方法
LL型失衡	current.bf>1 && current.left.bf>0	LL_right_rotate
LR型失衡	current.bf>1 && current.left.bf<0	LR_left_right_rotate
RR型失衡	current.bf<-1 && current.right.bf<0	RR_left_rotate
RL型失衡	current.bf<-1 && current.right.bf>0	RL_right_left_rotate
由上，我们可以得出调整失衡的函数如下:
//node为当前失衡节点 avl_node_ptr re_balance(avl_node_ptr node){ if (!node) return node; int bf=get_bf(node); int bf_l=get_bf(node->left); int bf_r=get_bf(node->right); if(bf>1 && bf_l>0) node=LL_right_rotate(node); if(bf>1 && bf_l<0>) node=LR_left_right_rotate(node); if(bf<-1 && bf_r<0) node=RR_left_rotate(node); if(bf<-1 && bf_r>0) node=RL_right_left_rotate(node); return node; }

有了上面的一些工具函数和平衡调整函数并且利用递归我们可以非常容易的实现插入和删除操作。

插入

avl_node_ptr avl_insert(avl_node_ptr node,int k){
    if(!node){
        node=new avl_node;
        node->key=k;
        node->height=1;
        node->left=NULL;
        node->right=NULL;
        return node;
    }
    if(k<node->key)
        node->left=avl_insert(node->left,k);
    else if(k>node->key)
        node->right=avl_insert(node->right,k);
    else{
        cout<<"can't insert a key that already esixt!"<<endl;
        return node;
    }
    //先调整高度，然后再平衡
    node->height=max(get_height(node->left),get_height(node->right))+1;
    node=re_balance(node);
    return node;
}

删除

avl_node_ptr  avl_delete(avl_node_ptr node,int k){
    if(!node)
        return node;
    if(k<node->key)
        node->left=avl_delete(node->left,k);
    else if(k>node->key)
        node->right=avl_delete(node->right,k);
    else{
        //找到需要删除的节点
        if(node->left==NULL||node->right==NULL){
            //删除的节点只有一个孩子或者没有孩子
            avl_node_ptr temp=(node->left==NULL)?node->right:node->right;
            if(temp==NULL){
                //没有孩子的情况
                temp=node;
                node=NULL;
            }
            else{//一个孩子
                node=temp;
            }
            delete temp;
        }
        else{
            //删除的节点有两个孩子
            avl_node_ptr temp=node->right;
            while(temp->left!=NULL)//找到node的右子树的最小关键字节点
                temp=temp->left;
            node->key=temp->key;
            node->right=avl_delete(node->right,temp->key);
        }
    }
    if(node==NULL)
        return node;
    node->height=max(get_height(node->left),get_height(node->right))+1;
    return re_balance(node);
}

参考

GeeksforGeeks
btechsmartclass
【算法】论平衡二叉树（AVL）的正确种植方法